데이터 프레임 정렬
worms <- read.csv("worms.csv")
names(worms)
attach(worms) ## worms의 변수들을 $없이 사용가능
worms[order(Area),] ## Area값이 작은 것부터 큰 순서대로 나열
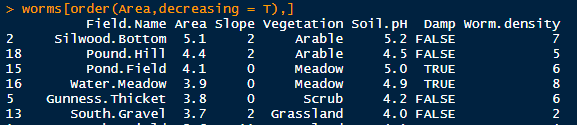
worms[order(Area,decreasing = T),] ## Area 값이 큰 것부터 작은 순서대로
#위와 같은 결과로
worms[rev(order(Area)),] ## Area 값이 큰 것부터 작은 순서로
설명변수 기준의 요약
aggregate : 데이터 프레임에서 양적인 정보를 요약하기 위해 필요한 함수
: 동시에 모든 연속형 변수의 평균값을 보고 싶을 때 사용
: 보고싶은 변수의 열 번호를 입력해야한다.
: 결과가 있는 행만 보여준다. (NA 인 경우 그 행은 제외한다.)
aggregate(worms[,c(2,3,5,7)],list(Vegetation),mean)
# worms라는 데이터에서 Vegetation 변수는 식물 경작지를 뜻하며,
# 이 식물 경작지는 Arable, Grassland, Meadow, Orchard, Scrub로 이루어져있다.
# aggregate라는 함수를 사용하여 worms 데이터 프레임에서 2,3,5,7번째에 해당하는
# 열의 평균들을 각각 구할 것이며, 그룹을 나누는 기준은 Vegetation으로 하고,
# 평균(mean)값을 구한다.
with, tapply : 하나의 변수에 대해 평균을 구하고자 할 때
with : attach가 되어있지 않은 경우 데이터 프레임을 지정해주는 역할을 한다.
tapply : 요인(factor)의 수준(level)별로 특정 벡터에 함수 명령어를 동시에 적용한다. tapply(벡터, 요인, 함수)
: factor를 기준으로 그룹별로 나누어서 통계 분석을 보려할 때 유용하다.
: 결측조합에 대해 NA를 반환한다.
tapply(Worm.density,Vegetation,mean)
# Worm.density에 대해 Vegetation 별로 mean 값을 구하여라
with(worms,tapply(Worm.density,Vegetation,mean))
# worms라는 데이터에서 Worm.density에 대해 Vegetation 별로 mean 값을 구하여라
관계
두 변수가 연속형일 때 적합한 그래프 --> 산점도(scatter plot)
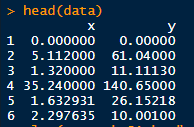
plot(x,y,pch=21,bg="red")
설명 변수가 범주형 변수인 경우 --> 박스 플롯(box plot)

plot(factor(month),upper)
# factor로 묶어주지 않고 month만 넣는 경우 scatter plot이 그려짐
# month를 범주형 변수로 보기 위해 그룹으로 인식시켜주는 factor를 넣어줌
위의 데이터에서 6월에 해당하는 데이터 중에 0으로 입력된 부분이 있다 이 부분을 NA로 고치려면???
which(upper==0 & month==6)
upper[4194] <- NA
plot(factor(month),upper)
연속형 변수들 사이에서의 상호작용
연속형 설명 변수의 경우 coplot을 이용해 상호작용을 확인 할 수 있으며, 범주형 설명변수의 경우에는 막대 그래프를 이용해 상호작용을 확인할 수 있다.

위와 같은 데이터가 있을 때, 연속형 설명변수는 x와 z 이고 반응변수는 y라고 하자.
같은 행에 두개의 그래프를 놓아본다.
windows(7,4)
par(mfrow=c(1,2))
plot(x,y)
plot(z,y)
이 그래프에서 반응변수와 설명 변수 사이의 명확한 상관관계를 볼 수 없었다.
연속형 설명 변수들 사이의 상호작용을 보기 위해 coplot을 사용해본다.
coplot --> z의 조건 아래에서 x에 대한 y의 값을 그린다.
plot(y~x|z)
# z값의 조건 아래에서 x값에 대응하는 y값을 그린다
coplot(y~x|z,pch=16,panel=panel.smooth)
# panel=panel.smooth --> 빨간색 선을 뜻한다.
위 그래프를 보면 반응변수(y)와 x사이에 명확한 연관성이 있고 이 형태가 z값에 따라 달라지는 것을 볼 수 있다.
z값이 작은경우(1) 강한 음의 상관관계를 가지며, z값이 큰 경우(6) y와 x는 강한 양의 상관관계를 가진다.
cf) 위의 회색 수평형 막대를 'shingle'이라 하고 변수 값의 범위를 나타낸다.
이 막대를 겹치지 않게 설정하고 싶으면, overlap=0을 사용하면 된다.
범주형 변수에서의 상호작용

위의 데이터는 하나의 연속형 반응 변수(yield)와 2개의 범주형 설명 변수(nitrogen, phosphorus)가 있는 데이터이며 범주형 설명변수는 2개의 수준(yes, no)을 가진다.

위 그래프를 통해 질소 비료와 인 비료에서의 주효과(main effect)를 볼 수 있다.
또한 인 비료보다 질소 비료가 좀 더 yield를 증가시킬 수 있어 보인다.
하지만 이 그래프에서 인 비료에 대한 반응이 질소 비료의 요인 수준에 의해 영향을 받는지에 대해서는 알 수 없다.
--> 반응의 4가지 수준(둘 다 없음, N만 있음, P만 있음, 둘 다 있음)에 대한 효과크기를 보여주는 interaction plot 필요

tapply를 이용해 평균을 구해봤을 때 열은 인 비료, 행은 질소 비료를 나타낸다.
- 인이 없을 때의 질소에 대한 효과크기를 구해보자.
효과크기 = 실험군과 대조군의 평균차이에 대한 표준화된 값
2.290/1.474=1.55 --> 인이 없을때, 질소도 없는 경우에서 질소 비료는 있는 경우를 나눠준다.
- 인이 있을 때의 질소에 대한 효과크기를 구해보자
3.480/1.876=1.86
질소비료에 대한 효과 크기는 인 비료의 수준(no, yes)에 의해 영향을 받는다.
--> 한 요인에 대한 반응이 다른 요인의 수준에 의해 영향을 받는다.
상호작용을 가장 효과적으로 보려면?? -->barplot
barplot(tapply(yield,list(nitrogen,phosphorus),mean),beside=TRUE,xlab="phosphorus")
legend(locator(1),legend=c("no","yes"),title="nitrogen",fill = c("black","lightgrey"))
위 그래프를 봤을 때, 인 비료와 질소 비료를 함께 처리 하는것이 좋다는 것을 알 수 있다.
'통계' 카테고리의 다른 글
| 크롤리 통계 - 4.1 분산 복습 (0) | 2021.01.19 |
|---|---|
| 크롤리 통계 - 4. 분산 (0) | 2021.01.18 |
| 크롤리 통계 - 3. 중심경향 (0) | 2021.01.12 |
| 크롤리 통계 - 1.1 (0) | 2021.01.12 |
| 크롤리 통계 - 1. 기본적인 사항 (0) | 2021.01.11 |



