베이즈 정리란 ~ 사전확률과 사후확률의 관계에 대한 설명

P(H|E) : 사후확률, 새로운 정보를 받은 후 갱신된 신뢰도
P(H) : 사전확률, 어떤 사건이 발생했다는 주장에 관한 신뢰도
H : 가설 또는 어떤 사건이 발생했다는 주장
E : 새로운 정보
즉, P(H) 에서 어떤한 정보를 받아 P(H|E) 로 갱신이 되는것
불확실성이나 경험적인 수치를 기반으로 하며 추가되는 정보를 바탕으로 사전확률을 갱신하다.
예시1)
질병A의 발병률은 0.1% 이다.
질병이 실제로 있을 때 질병이 있다고 진단할 확률(민감도, sensitivity)은 99%,
질병이 없을 때 없다고 진단할 확률(특이도, specificity)는 98% 라고 할 때,
어떤 사람이 질병에 걸렸다고 진단 받았을 때, 이 사람이 정말로 질병에 걸렸을 확률은????
질병A의 발병률은 0.1% --> P(H) = 0.001
질병이 실제로 있을 때 질병이 있다고 진단할 확률(민감도, sensitivity)은 99% --> P(E|H) = 0.99
질병이 없을 때 없다고 진단할 확률(특이도, specificity)는 98% --> P(E^c|H^c) =0.98
H = 실제로 병이 있다. TRUE다.
E = Positive로 출력, 병이 있다고 진단을 받았다.
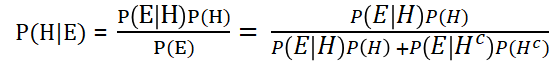
이 식으로 계산을 하면 P(H|E) = 0.047 이 나온다.
원래 알려진건 P(H)의 0.001인데 여러 증거를 통해 주장을 갱신한 것이다.
예시2)
예시1에서 한번 양성판정을 받았던 사람이 두번째 검진을 받고 또 양성판정을 받았을 때 이 사람이 실제로 질병에 걸린 확률은???
1에서 사후확률(P(H|E)) 이었던 값이 예시2에서는 사전확률(P(H))로 쓰여진다. --> P(H)= 0.047
P(H) = 0.047 , P(H^c) = 1-0.047 = 0.953
그리고 위의 P(H|E)를 구하는 식에 대입을 해보면~

값은 0.709 가 나오게 된다.
예시1에서 계산하여 얻은 확률에 근거를 기반으로 하여 한번 더 확률을 갱신하면 약 70%의 확률로 이 사람은 병에 걸렸을 수 있다고 말할 수 있다.
'통계' 카테고리의 다른 글
| 크롤리 통계 - 5. 하나의 표본 (0) | 2021.01.21 |
|---|---|
| 크롤리 통계 - 4.1 분산 복습 (0) | 2021.01.19 |
| 크롤리 통계 - 4. 분산 (0) | 2021.01.18 |
| 크롤리 통계 - 3. 중심경향 (0) | 2021.01.12 |
| 크롤리 통계 - 2 (R, 데이터프레임) (0) | 2021.01.12 |



