크롤리 통계 - 4. 분산

통계

크롤리 통계 - 4. 분산

BIJoy 2021. 1. 18. 19:51

분산

변량들이 퍼져있는 정도, 분산이 크면 들죽날죽 불안정하다는 의미

데이터의 퍼져 잇는 양상을 봐보자

-평균을 계산하고 그 평균과 데이터 사이의 거리(잔차;residual , 편차;deviation)를 보자

y <- c(13,7,5,12,9,15,6,11,9,7,12)
plot(y,ylim=c(0,20))
plot(1:11,y,ylim=c(0,20),pch=16,col="blue")
abline(h=mean(y),col="dark green")
# abline을 이용하여 수평선을 그릴건데 h --> 어떤 값을 이용할 것인가
for(i in 1:11) lines(c(i,i),c(mean(y),y[i]),col="red")
# 데이터 값으로부터 평균까지의 길이를 그려줌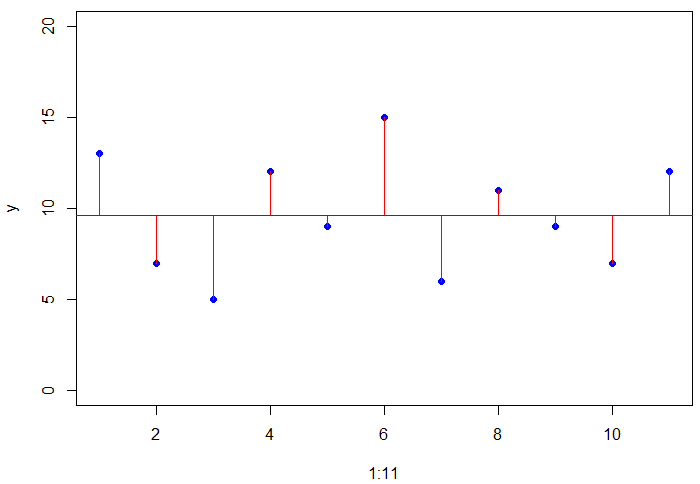

빨간선이 길수록 데이터의 변동선이 크다고 할 수 있다.

(-) 경우는 어떻게 계산을 할까?? --> 잔차의 제곱을 이용한다. (절댓값을 이용한 경우에는 미분이 불가능한 부분이 생길 수 있기 때문에) --> 이것을 제곱합(sum of squares)라고 한다.

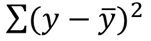
이렇게 제곱합을 구했는데... 데이터가 추가된다면??

제곱합은 커지게 된다 --> 표본 수가 변동성의 측정치에 영향을 주는 것은 바람직하지 않다.

--> 제곱합은 표본 수로 나눠 평균 제곱 편차(mean squared deviation)를 구한다

제곱합의 공식에서 표본평균(y_bar)은 데이터로부터 추정해야 하는 모수다.

cf) 모수 : 관심의 대상이 되는 모집단 특성 (평균, 표준편차 등...)

따라서 평균 제곱 편차를 계산할 때 표본크기 n이 아닌 자유도 n-1 로 제곱합을 나눠야 한다.

- 자유도를 이용해 계산이 이뤄져야 분산의 unbiased estimate(기댓값이 모수와 동일한 추정량)를 얻을 수 있다.

모집단의 평균 --> 표본평균의 평균으로 추정

모집단의 분산 --> 표본분산의 평균으로 추정

--> 이렇게 평균으로 모수를 처정하는 값 = 추정량

위에서 추정량은 표본평균 , 표본분산

이 추정량과 실제 모수와의 차이 = bias

R에서 분산을 계산하는 함수 = var(y)

분산 예제

다음과 같은 데이터가 있다.

gardenA와 gardenB는 평균은 다르지만 분산은 같다

gardenB와 gardenC는 평균은 같지만 분산이 다르다

--> 분산이 통계적으로 의미 있게 다르다고 할 수 있을까?

--> 큰 수치의 분산을 작은 수치의 분산으로 나눠 F 검정을 시행한다.

10.66667이 나온다.

두 분산이 실제로 같다고 할 때 10.66667보다 더 큰 값을 얻게 될 확률

--> F 분포의 누적 확률이 필요 --> pf 사용

R의 내재함수 사용해 F검정 시행

0.001624로 0.05(5%)보다 작으므로

두 분산 간에 통계적으로 유의한 차이가 있다고 결론 내릴 수 있다.

cf)

num df = 분자의 자유도

denom df = 분모의 자유도

분자와 분모에 오는 값은 분산 구한다면서 평균을 사용했기 때문에 자유도가 9

gardenA 와 gardenB는 평균이 다르지만 분산은 같다.

분산이 같은 경우!!

- 2개의 평균을 비교할 때 --> t-test

- 3개 이상의 평균을 비교할 때 --> ANOVA

등분산은 대부분의 통계 분석에서 가장 중요한 가정

분산이 다르다면 평균을 비교해서는 안된다.

분산과 표본크기

sample size가 클수록 분산이 작아진다

표본의 수가 작은 경우 분산의 변화가 심할 수 있다.

분산의 사용

분산을 사용하는 2가지 주요한 목적

- 비신뢰도의 측정

- 가설 검정

비신뢰도의 측정

분산(s^2)이 커질수록 비신뢰도도 커진다. (비례관계)

표본의 크기(n)가 커질수록 비신뢰도는 작아진다. (반비례관계)

분산의 차이의 제곱합에 기초 하므로 --> 평균의 단위가 cm라면 분산은 cm^2이 됨

따라서 단위를 맞춰주기 위해 비신뢰도의 공식에 제곱근 기호가 필요

이러한 비신뢰도의 측정치가 표준오차

평균의 표준오차(SE)

추정값으로부터 표본들의 통계량이 흩어져 있는 정도

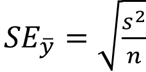
R을 이용해 gardenA의 표준오차를 구해보자

sqrt(var(gardenA)/10)  #표본 수 = 10

0.3651484 가 나온다.

--> 요약 : gardenA의 평균 오존 농도는 3.0 ± 0.365pphm 이다

신뢰구간

표본 추출이 반복해서 이뤄졌을 때 평균이 놓일 수 있는 범위

비신뢰도가 크면 신뢰구간도 넓어진다.

표본의 크기가 정규분포를 적용하기에 너무 작은경우 (n < 30) --> 스튜던트 t분포를 사용한다.

여러 신뢰 수준에 대한 스튜던트 t 분포의 값은 qt 함수를 사용하면 확인 --> t 분포의 분위수(quantile)를 반환

신뢰구간은 항상 양측으로 제시

95% 신뢰구간을 계산하려면 α=0.025의 스튜던트 t 분포 값을 알아야 한다.

분포의 왼쪽부터 0.025와 오른쪽 0.975에 대해 각각 계산이 이뤄져야 한다.

qt(.025,9)
# -2.262157
qt(.975,9)
# 2.262157

qt 함수의 첫번째는 확률이고 두번째는 자유도

-2.262 지점이 0.025 확률 , 2.262 지점이 0.975 확률

신뢰의 정도가 증가함에 따라 (95% --> 99% --> 99.5%) 신뢰구간의 폭이 증가한다.

표준오차는 신뢰 수준에 의해 영향을 받지 않는다.

표본 수가 작은 경우(n<30) 평균의 신뢰구간은 다음과 같은 공식으로 요약할 수 있다.

신뢰구간을 구할 때 표준오차의 앞에 통계치를 넣어주는데 구하고자 하는 평균에 대한 분포의 통계치를 넣어준다.

아래는 t분포의 통계치에 관련한 값이다.

신뢰구간 = t값(분포에 대한 값) X 표준오차

부트스트랩

신뢰구간을 계산하는 또 다른 방법

n개의 측정치를 가진 하나의 표본이 있다. 이 표본으로부터 많은 방식으로 다시 표본 추출을 할 수 있다.

이때, 복원이 가능한 추출을 가정한다. 그리고 각 표본의 평균을 계속해서 계산 --> 이렇게 얻어진 평균들을 가지고 신뢰구간을 구한다.

resampling with replacement

하나의 sample을 모집단으로 생각해서 이 sample로부터 또 sampling을 하는 것

부트스트랩 만드는 코드

data <- read.csv("skewdata.csv")
attach(data)
plot(c(0,30),c(0,60),type="n",xlab="Sample size",ylab="Confidence interval")
for(k in seq(5,30,3)){
  a <- numeric(10000)
  for(i in 1:10000){
    a[i] <- mean(sample(values,k,replace=T))
  }
points(c(k,k),quantile(a,c(.025,.975)),type="b",pch=21,bg="red")
}

검정수직선이 신뢰구간을 나타냄

표본크기가 20이 넘기 전까지는 신뢰구간이 급속하게 좁아지는 것을 볼 수 있다.

n=30일때, quantile 함수를 이용해 신뢰구간의 범위를 지정

quantile(a,c(0.025,0.975))

2.5% 97.5%

24.79751 37.99601